SM3 密码杂凑算法

SHA-256 是常用的哈希算法，输入长度小于 2^64 bit 的消息，输出为 256 bit 的杂凑值，分组大小为 512 bit，字长定义为 32 bit ；

SM3 算法在 SHA-256 的基础上进行改良，输入长度小于 2^64 bit 的消息，输出为 256 bit 的杂凑值。分组大小为 512 bit，字长定义为 32bit ；

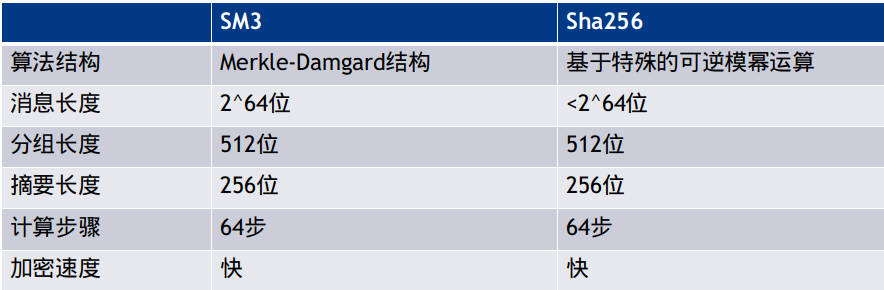
SM3 和 SHA-256 对比：

SM3 算法步骤

SM3 算法主要分为以下几个部分：

消息填充
消息扩展
迭代压缩
生成杂凑值

输出为 256 bit 杂凑值，即 32 byte

设消息 m 的长度为 l ，索引从 0 开始编号

常量与函数

符号约定

ABCDEFGH：8 个字寄存器（串联）

$ B^{(i)} $：第 i 个消息分组

CF：压缩函数

$ FF_j $：布尔函数，随 j 的变化取不同的表达式

$ GG_j $：布尔函数，随 j 的变化取不同的表达式

IV：初始值，用于确定压缩函数寄存器的初态

$ P_0 $：压缩函数中的置换函数

$ P_1 $：消息扩展中的置换函数

$ T_j $：常量，随 j 的变化取不同的值

$ m $：消息

$ m’ $：填充后的消息

$ \wedge $：32 比特与运算

$ \vee $：32 比特或运算

$ \oplus $：32 比特异或运算

$ \lnot $：32 比特非运算

$ + $：$ mod 2^{32} $ 算数加运算

$ \lll k $：循环左移 k 比特运算

$ \leftarrow $：左向赋值运算符

初始值 IV

$$ IV = 7380166f 4914b2b9 172442d7 da8a0600 a96f30bc 163138aa e38dee4d b0fb0e4e $$

常量

$$
T_j =
\begin{cases}
79cc4519 & {0 \leq j \leq 15} \newline
7a879d8a & {16 \leq j \leq 63}
\end{cases}
$$

布尔函数

$$
FF_j(X, Y, Z) =
\begin{cases}
X \oplus Y \oplus Z & {0 \leq j \leq 15} \newline
(X \wedge Y) \vee (X \wedge Z) \vee (Y \wedge Z) & {16 \leq j \leq 63}
\end{cases}
$$

$$
GG_j(X, Y, Z) =
\begin{cases}
X \oplus Y \oplus Z & {0 \leq j \leq 15} \newline
(X \wedge Y) \vee (\lnot X \wedge Z) & {16 \leq j \leq 63}
\end{cases}
$$

X，Y，Z 为字。

置换函数

$$
P_0(X) = X \oplus (X \lll 9) \oplus (X \lll 17) \newline
P_1(X) = X \oplus (X \lll 15) \oplus (X \lll 23)
$$

X 为字。

消息填充

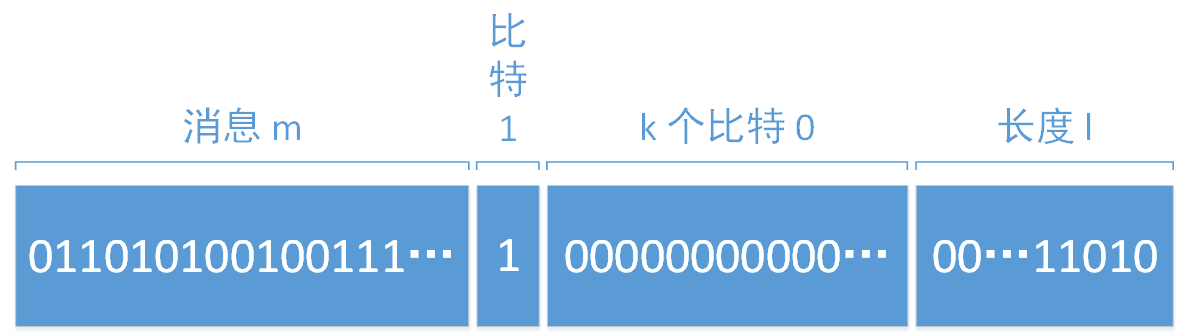
首先在消息 m 的末尾添加一个比特 1 ；

然后再添加 k 个比特 0 ；

k 满足 l + 1 + k ≡ 448(mod 512) ，字节表示为 (448(mod 512))/8 = 56(mod 64)

最后添加长度 l 的二进制比特表示，以大端序存放；

数据的高位字节存储在地址的低端

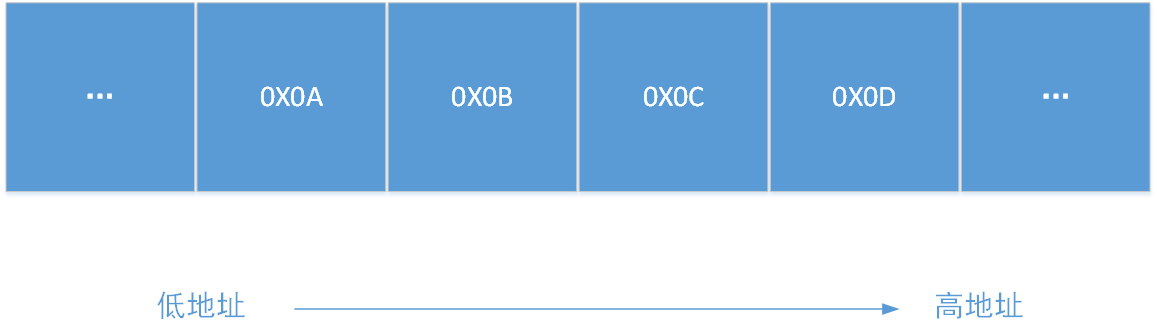
填充后的消息 m’ 的长度为 512 bit 的倍数。

消息扩展

将填充后的消息 m’ 按照 512 bit 分组

n = (l + k + 65) / 512

$$ m’ = B^{(0)}B^{(1)}…B^{(n-1)} $$

对消息分组 $ B^{(i)} $ 进行扩展，生成 132 个字：

$$
W_0, W_1, …, W_{67}, W_0’, W_1’, …, W_{63}’
$$

具体过程如下：

首先将消息分组 $ B^{(i)} $ 划分为 16 个字 $ W_0, W_1, …, W_{15} $ ，记为 $ W_j $
递推生成剩余的 $ W_j $ ，共计 68 个字
$$
\begin{align}
& FOR \quad j=16 \quad TO \quad 67 \newline
& \qquad W_j \leftarrow P_1(W_{j-16} \oplus W_{j-9} \oplus (W_{j-3} \lll 15)) \oplus (W_{j-13} \lll 7) \oplus W_{j-6} \newline
& ENDFOR
\end{align}
$$
递推生成 $ W_j’ $ ，共计 64 个字
$$
\begin{align}
& FOR \quad j=0 \quad TO \quad 63 \newline
& \qquad W_j’ = W_j \oplus W_{j+4} \newline
& ENDFOR
\end{align}
$$

迭代压缩

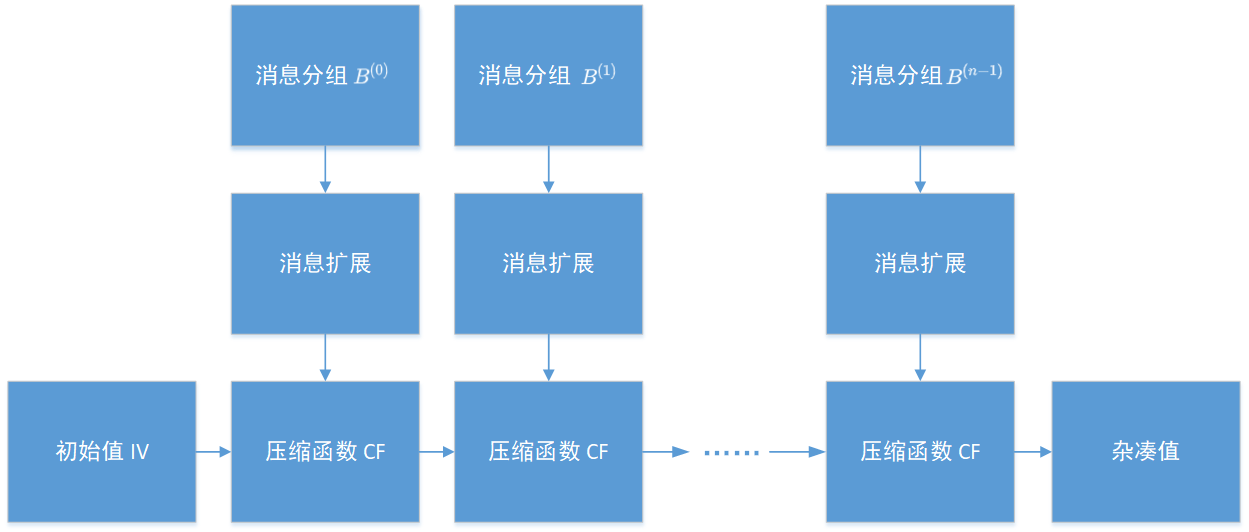
迭代过程

$$
\begin{align}
& FOR \quad i=0 \quad TO \quad n-1 \newline
& \qquad V^{(i+1)} = CF(V^{(i)}, B^{(i)}) \newline
& ENDFOR
\end{align}
$$

CF 是压缩函数
$ V^{(0)} $ 为 256 比特初始值 IV
$ B^{(i)} $ 为填充后的消息分组
迭代压缩的结果为 $ V^{(n)} $ ，即最终的杂凑值

压缩函数

A, B, C, D, E, F, G, H 为字寄存器
SS1, SS2, TT1, TT2 为中间变量
$ V^{i+1} = CF(V^{(i)}, B^{(i)}) , 0 \leq i \leq n-1 $

压缩函数过程如下：

$$
\begin{align}
& ABCDEFGH \leftarrow V^{(i)} \newline
\newline
& FOR \quad j=0 \quad TO \quad 63 \newline
& \qquad SS1 \leftarrow ((A \lll 12) + E + (T_j \lll j)) \lll 7 \newline
& \qquad SS2 \leftarrow SS1 \oplus ((A \lll 12) \newline
& \qquad TT1 \leftarrow FF_j(A, B, C) + D + SS2 + W_j’ \newline
& \qquad TT2 \leftarrow GG_j(E, F, G) + H + SS1 + W_j \newline
& \qquad D \leftarrow C \newline
& \qquad C \leftarrow B \lll 9 \newline
& \qquad B \leftarrow A \newline
& \qquad A \leftarrow TT1 \newline
& \qquad H \leftarrow G \newline
& \qquad G \leftarrow F \lll 19 \newline
& \qquad F \leftarrow E \newline
& \qquad E \leftarrow P_0(TT2) \newline
& ENDFOR \newline
\newline
& V^{(i+1)} \leftarrow ABCDEFGH \oplus V^{(i)}
\end{align}
$$

生成杂凑值

$$ ABCDEFGH \leftarrow V^{(n)} $$

输出 256 bit 杂凑值 y = ABCDEFGH

总结

SM3 算法流程简洁明了，可以直接按步骤实现。已有支持国密SM2/SM3/SM4/SM9/ZUC/SSL的密码工具箱 The GmSSL Project ，提供不同语言的 API 接口；学习 Golang 的过程中找到开源实现基于Go语言的国密SM2/SM3/SM4加密算法库，研读了一段时间，现在才回头梳理总结（老懒熊了xd