Datalog 引擎 Soufflé 指南
前言
前段时间看 Doop 顺手整理了篇 LogiQL 入门,现在整理一下 Soufflé 的使用记录。Soufflé 是一款开源的 Datalog 引擎,相对 LogixBlox 更新更快(至少有论文这么总结),而 Doop 默认使用和维护了一整套 Soufflé 的规则。因为是开源引擎,所以有相关工作直接对 Doop 和 Soufflé 进行修改,用于实现一些分析,然后发了顶会😇😇😇
相关资料真的是少,不然就是难读,反正花时间看呗(摊手),最终目的是看懂 Doop 中的规则。
安装 Soufflé
实验使用 Ubuntu 20.04 进行,souffle、doop(java8)都可以成功安装和使用。
Soufflé 有一个解释器和一个编译器来执行 Datalog 程序,通过脚本安装。PS:万一无法下载,可能是服务器问题(之前也宕机过)
1 | # 下载 |
使用 Soufflé
一个简单的例子
example.dl 定义“边”和“路径”
edge是一个.input关系,将从磁盘读取path是一个.output关系,将被写入磁盘- 如果有一条从 x 到 y 的边,那么就有一条从 x 到 y 的路径
- 如果有一条从 x 到 z 的路径,并且从 z 到 y 有一条边,那么就有一条从 x 到 y 的路径
1 | .decl edge(x:number, y:number) // 声明 |
如果输入的 edge 关系是图中的顶点对,根据上面的两个规则,输出的路径关系将提供所有顶点对 x 和 y,即图中存在 x 到 y 的路径。
输入文件 edge.facts,使用制表符分隔:
1 | 1 2 |
执行分析,-F 表示输入文件路径,-D 表示输出文件路径:
1 | souffle -F. -D. example.dl |
查看输出文件 path.csv,包含所有存在路径的顶点对:
1 | 1 2 |
上面运行的是 解释器模式,Soufflé 还支持 编译器模式,将 Datalog 程序转换为 C++ 程序,然后编译生成可执行文件,使用 -o 参数:
1 | # 生成可执行文件 |
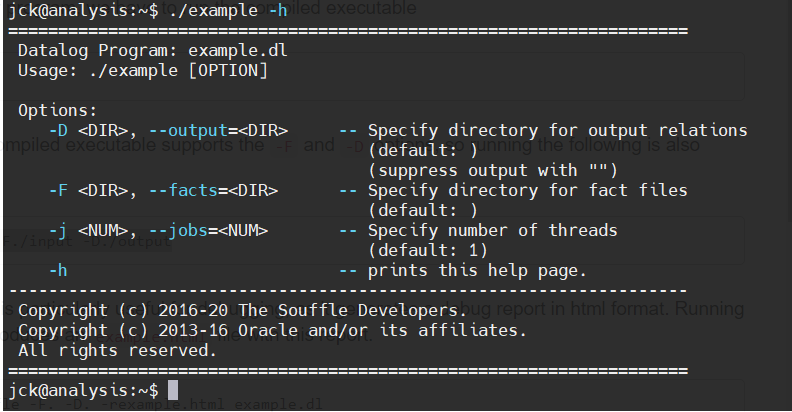
-r 参数用于调试,生成 HTML 格式的调试报告 example.html:
1 | souffle -F. -D. -rexample.html example.dl |
-p 参数用于分析,以下命令将创建一个包含分析信息的日志文件 example.log:
1 | souffle -F. -D. -pexample.log example.dl |
souffle 还提供了一个命令行工具 souffleprof,可用于分析 example.log:
1 | souffleprof example.log |
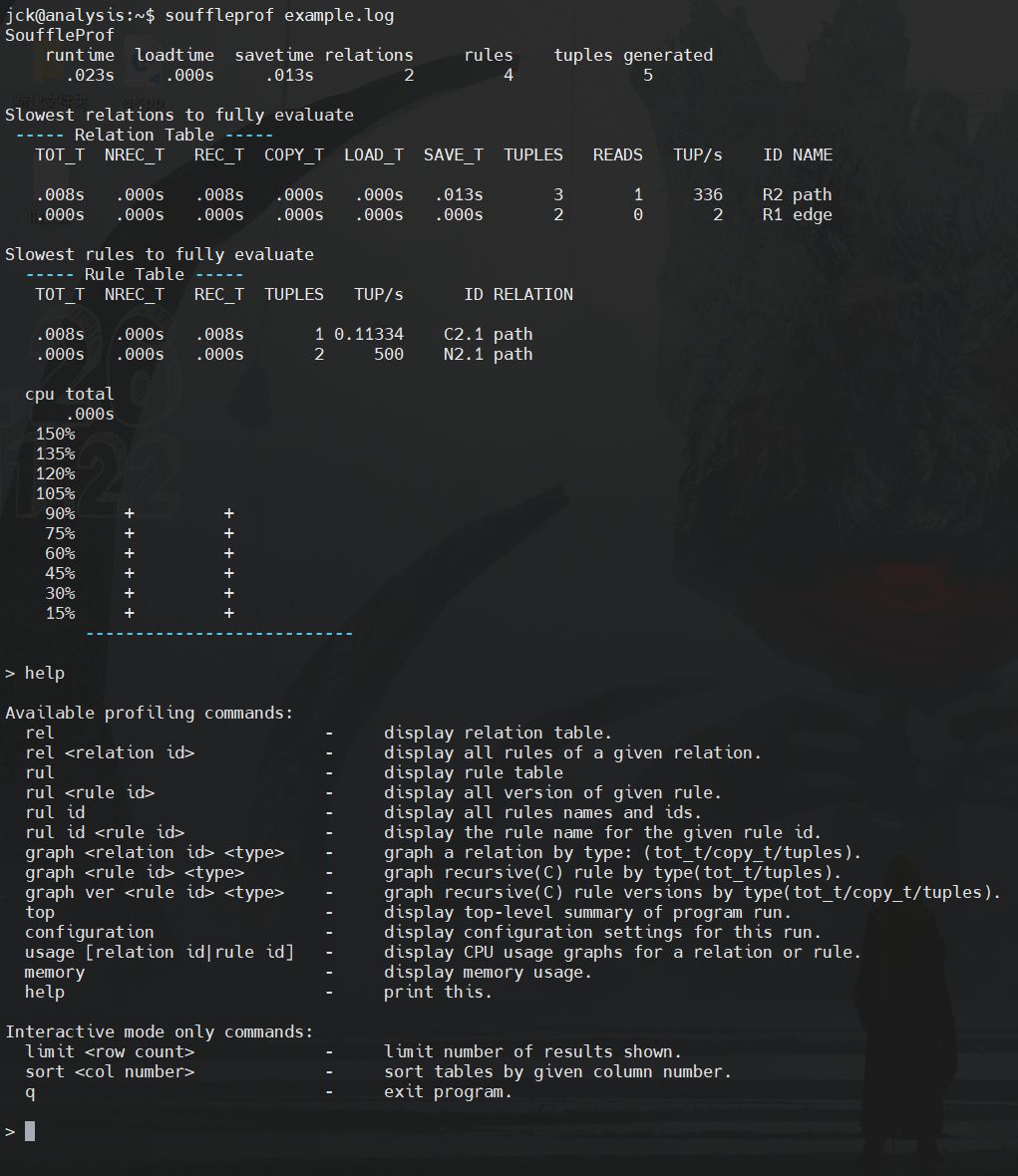
例1
Datalog 是一种(声明式)基于逻辑的查询语言,允许用户执行递归查询。Datalog 语法的规范没有统一的标准,通常采用 Prolog 风格的语法。Soufflé 的语法受到 Datalog 实现的启发,即 Z3 中的 bddbddb(BDD-Based Deductive DataBase) 和 muZ。
Soufflé 为大规模面向逻辑的编程提供了软件工程功能(例如组件),对于实际使用,Soufflé 通过算术函子(arithmetic functors)扩展了 Datalog 使其图灵等价,让程序员能够编写非终止的程序。
- 非终止的一个例子是事实 A(0) 和规则 A(i + 1) :- A(i),没有额外的约束
- 这导致 Soufflé 尝试输出无限数量的关系 A(n),其中 n >= 0
- 这在某种程度上类似于 C 等命令式编程语言中的无限 while 循环。但是,算术函子提供的表达能力增强非常方便编程。
传递闭包
集合 X 上的关系 R 是可传递的,如果对于 X 中的所有 x、y、z,当 x R y 且 y R z 则 x R z。下面的示例表示有向图,其中边定义关系,如果元组满足以下两个规则中的任何一个,则元组处于传递闭包(可达关系)中。
- 实际上,edge 中的所有元素都是可达的(根据基本规则),归纳规则捕获了传递属性,包括像
reachable("a", "d")这样的元组。
1 | .decl edge(n: symbol, m: symbol) |
同代
给定一棵树(具有特定根节点的有向无环图),目标是找到哪些节点处于同一级别。
- 下图中节点 b 和 c 处于同一级别,节点 e 和 g 也处于同一级别。
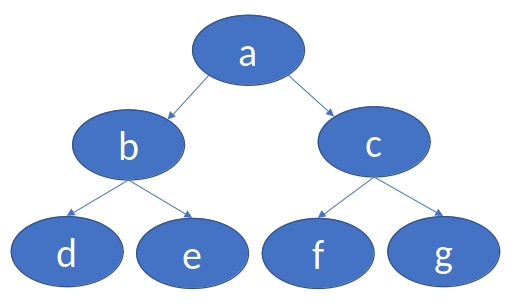
定义 Parent 关系,然后描述这棵树;定义 Person 关系和 SameGeneration 关系
1 | .decl Parent(n: symbol, m: symbol) // 子代,父代 |
数据流分析
数据流分析(Data-flow analysis, DFA)旨在确定程序的静态属性,基于控制流图(Call Flow Graphs, CFG),根据节点和图的属性进行程序分析。
一个例子是可达性定义(reaching definition):变量的定义是否到达程序中特定的点。因为变量的赋值可以直接影响程序中另一点的值,这里考虑变量 v 的明确定义 d:
1 | d: v = <expression>; |
如果从 d 到 u 的所有路径都不包含 v 的任何明确定义,则变量 v 的定义 d 被认为可到达语句 u。注意即使没有明确的定义,函数也可能对变量产生副作用。
考虑以下控制流图,包含变量 v 的明确定义 d1 和 d2,只有 d2 定义的 v 能达到 B3。
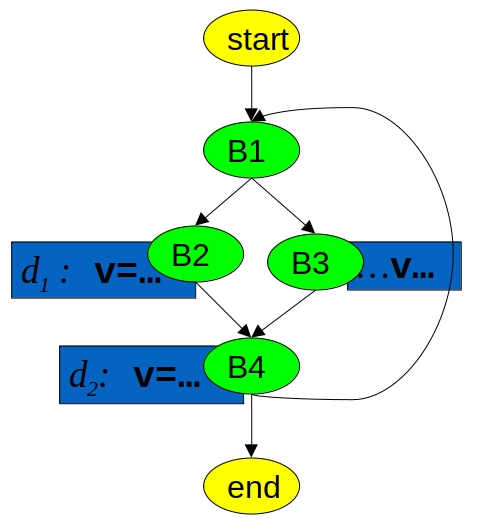
以下代码输出 CFG 的所有阶段,其中 v 可能被这些定义之一捕获。
1 | // define control flow graph |
关于输入和 C 预处理器的备注
与 C++ 一样,Soufflé 使用两种类型的注释:
- 类型 1:
// 这是备注 - 类型 2:
/* 这也是备注 */
C 预处理器处理来自 Soufflé 的输入(即可以使用宏),例如:
1 | #include "myprog.dl" |
例2:关系
关系定义
关系必须声明后才能使用,在 Soufflé 代码中编写代码行的顺序不会影响程序的正确性。使用两个字段 a 和 b 声明关系 edge,每个字段都是符号(字符串)。
1 | .decl edge(a:symbol, b:symbol) |
I/O 指令
用户可以指定用于加载输入和将输出写入文件的指令:
- 输入指令
.input <relation-name>从<relation-name>.facts读取,默认情况下由制表符分隔 - 输出指令
.output <relation-name>写入文件,通常是<relation-name>.csv(默认)或 stdout(取决于选项) - 打印关系大小指令
.printsize <relation-name>将给定关系的基数(cardinality)打印到标准输出。
1 | .decl A(n: symbol) |
关系可以从以下文件加载或写入以下文件:
- 任意 CSV 文件
- 压缩的文本文件
- SQLite3 数据库
例如,要将评估后的关系存储到 SQLite3 数据库中,用户可以指定如下内容:
1 | .decl A(a:number, b:number) |
目标
Datalog 中的目标是形式为 false <= p 的逻辑关系,其中 p 是逻辑关系。在 Soufflé 中目标是由输出指令模拟的,优点是可以在一次 Soufflé 程序的执行中评估多个独立的目标。
语法便利
可以编写具有多个头的规则,这是一种语法糖,可以最大限度地减少编码工作。下面是一个利用此功能的代码片段以及未应用转换的等效代码:
1 | // Multiple heads |
类似地,规则体中的析取(disjunctions)也可以作为语法糖,例如:
1 | // Disjunction in rule bodies |
例3:属性的类型系统
Soufflé 的类型系统是静态的,就像 C 之类的语言一样,而与 Python 之类的语言不同。必须在编译(或解释)之前定义关系的属性,并在编译时检查类型。让程序员清楚地了解关系的定义及其用法,在运行时不进行动态检查能够最大限度地减少评估时间。
原子类型
Soufflé 有两种基本类型,符号类型 symbol 和数字类型 number。符号类型包含所有字符串,在内部由一个序数(ordinal number)表示。值 ord("hello") 对应于给定程序的这个序数,在这种情况下是字符串 “hello”。数字类型包括所有数字的全域。
例4:算术表达式
Soufflé 允许算术函子,扩展了传统的 Datalog 语义,函子中的变量可能不包含任何自由变量。一个简单的例子,最后一行连接中的第二个条件调用了算术运算符 <:
1 | .decl A(n: number) |
打印斐波那契数列:
1 | .decl Fib(i:number, a:number) |
Soufflé 中允许使用以下算术函子:
- 加法:
x + y - 减法:
x - y - 除法:
x / y - 乘法:
x * y - 模数:
a % b - 幂:
a ^ b - 计数器:
autoinc() - 位操作:
x band y、x bor y、x bxor y和bnot x - 逻辑运算:
x land y、x lor y和lnot x
Soufflé 中允许以下算术约束:
- 小于:
a < b - 小于或等于:
a <= b - 等于:
a = b - 不等于:
a != b - 大于或等于:
a >= b - 大于:
a > b
在源码中,数字可以写成十进制、二进制和十六进制:
1 | .decl A(x:number) |
数字编码
数字可以用作逻辑值,如在 C 中:
0代表假!= 0代表真
因此,它们可用于逻辑运算 xland y、x lor y 和 lnot x:
1 | .decl A(x:number) |
函子 autoinc()
函子 autoinc() 在每次求值时都会产生一个新数字,但是不允许在递归关系中使用。可用于为符号创建唯一编号(充当标识符),例如:
1 | .decl A(x: symbol) |
给定一个集合 A(x:symbol),创建一个后继关系 Succ(x:symbol, y:symbol) 使得第一个参数包含 A 中的元素 x,第二个参数包含 x 的后继,这也是一个 A 的元素。
例如,集合 A = {"a", "b", "c", "d"} 具有后继关系 Succ=(("a", "b"), ("b", "c"), ("c", "d")}。假设一个元素(在这种情况下是一个符号)的总顺序根据它的序数计算,内部表示为一个数字。
1 | .decl A(x:symbol) input // 集合 |
计算后继关系的第一个和最后一个元素。
1 | .decl First(x: symbol) output |
例5:聚合
Soufflé 中的聚合是指使用特定的函子来汇总有关查询的信息,聚合类型包括计数、求最小值/最大值、求和。在 Soufflé 中,信息通常不能从子目标(聚合函子的参数)流到外部作用域。例如,如果希望找到关系 Cost(x) 的最小值,无法找到使成本最小化的特定 x 值,因为这样的 x 值可能不是唯一的。
计数
计数函子用于计算子目标的集合大小,语法为 count:{<sub-goal>}。
以下示例输出“蓝色”汽车的数量,即 Car 中第二个参数为“蓝色”的元素数量:
1 | .decl Car(name: symbol, colour:symbol) |
最大值/最小值/求和
max 函子输出集合的最大值,语法为 max <var>:{<sub-goal(<var>)>}。
1 | .decl A(n:number) |
最小值语法为 min <var>:{<sub-goal>(<var>)>};求和语法为 sum <var>:{<sub-goal>(<var>)>}。
Soufflé 程序
主要整理 Doop 中用到的一些内容,包括基本的关系、类型、规则,以及进阶的自定义函子、组件、编译指令。(这不是全包含了吗😅)
- 语言(Language)
- 关系(Relations)
- 类型(Types)
- 规则(Rules)
- 组件(Components)
- 用户定义函子(User-Defined Functors)
- 编译指令(Pragma)
组成
语言
Soufflé 中的主要语言元素是关系声明(relation declarations)、事实(facts)、规则(rules)和指令(directives)。
例如,以下程序中包含两个关系 A 和 B,关系必须声明(以便编译时检查属性的使用);关系 A 有两个事实:A(1,2). 和 A(2,3).,事实是无条件成立的规则,即事实是 Horn Clause A(1,2) ⇐ true;关系 B 有两个规则:B(x,y) :- A(x,y). 和 B(x,z) :- A(x,y), B(y,z).,表示 Horn Clause B(x,y) ⇐ A(x,y) 和 B(x,y) ⇐ A(x,y), B(y,z)。
- Horn Clause 的解释可以看:http://www.blogjava.net/Javawind/archive/2007/12/12/167108.html
最后的指令 .output B 表示在执行结束时查询关系 B,并将其写入文件或打印到屏幕中。关系声明、事实、规则和指令的顺序可以是任意的,并不影响最终的执行。
1 | .decl A(x:number, y:number) // declaration of relation A |
关系
Soufflé 要求声明关系,关系是一组有有序元组 (x1, ..., xk),其中每个元素 xi 都是由类型定义的数据域的成员。以下声明定义了仅包含数字对的关系 A,第一个属性被命名为 x,第二个属性被命名为 y,两个属性的类型都是数字。
1 | .decl A(x:number, y:number). |
Soufflé 的类型检查器将推断规则中的变量类型,并检查它们是否正确使用。
类型
Soufflé 利用类型化的 Datalog 方言进行静态检查,从而能够提早发现查询规范中的错误。必须为关系的任何属性指定类型,Soufflé 中有四种原始类型:符号(symbol)、数字(number)、无符号数字(unsigned)、浮点数(float)。
规则
规则是条件逻辑语句,以头部开始,然后是身体。例如,如果一对 (x, y) 在 B 中则 A 成立:
1 | A(x,y) :- B(x,y). |
组件
Soufflé 有组件这个概念,可用于模块化大型逻辑程序。一个组件可能包含其他组件、关系、类型声明、事实、规则和指令;组件必须声明和实例化后才可以使用,每个组件都有自己的命名空间;组件可以继承一个或多个超级组件。
用户定义函子
可以使用用户定义函子扩展 Soufflé,用户定义函子用 C/C++ 实现。用户定义函子有两种风格:朴素函子和有状态的函子,有状态的函子公开记录和符号表。
编译指令
用编译指令配置 Soufflé,例如,可以在源码中设置命令行选项。
组件 Components
组件是程序的模块化部分,可以封装元素,包括关系声明、类型声明、规则、事实、指令和其他组件。组件包含声明和实例化两个操作。
使用 .comp 关键字声明组件,组件包含的元素定义在 {...} 内:
1 | .comp MyComponent { |
使用 .init 关键字初始化组件,在内部,Soufflé 将组件实例扁平化(flatten),并为每个组件实例创建命名空间,因此要用限定名称调用其中的元素。
1 | .init myInstance1 = MyComponent // 实例化 |
对于上面的例子,Soufflé 在内部对组件实例进行了如下扩展:
1 | .type myInstance1.myType = number |
可以使用 souffle --show=transformed-datalog xxx.dl > expansion.dl 生成扩展后的 datalog 文件。
下面定义了两个 MyComponent 实例:
1 | .init myInstance1 = MyComponent |
Soufflé 在内部生成以下逻辑程序,通过前缀避免名称冲突:
1 | .type myInstance1.myType = number |
如果规则/事实在没有关系声明的组件中定义,Soufflé 不会预先添加前缀,而是会将解析推迟到实际的组件实例化。
1 | .decl Out(x:number) |
Soufflé 会将代码扩展,实际会是这样:
1 | .decl Out(x:number) |
如果规则和事实在本地作用域中被实例化,那么前缀将被预先添加到前面。
类型参数化
组件可以通过未限定的类型名称进行参数化,下面的例子实例化了两个不同的类型的组件:
1 | .comp ParamComponent<myType> { |
在内部,Soufflé 将显式实例化不同属性的组件:
1 | .decl numberInstance.TheAnswer(x:number) // relation of numberInstance |
组件名称也可以用参数传递,例如,实例化时指定生成组件 One:
1 | .decl R(x:number) |
在内部将生成以下程序:
1 | .decl R(x:number) |
继承
一个组件可以继承多个超级组件,超级组件的元素将被传递给子组件。使用 : 继承超级组件,用 , 分隔:
1 | .comp Base1 { |
组件 Base1 和 Base2 将所有组件元素传递给子组件 Sub,在内部实例化 mySub 时生成以下代码:
1 | .type mySub.myNumber = number |
可重写的关系
如果在超级组件中将关系声明为可覆盖(overridable),则子组件可以重写关联的规则和事实。例如
1 | .comp Base { |
子组件丢弃事实 R(1). 和规则 R(x+1) :- R(x), x < 5.,然后进行重写,在内部实例化 mySub 时生成以下代码:
1 | .decl mySub.R(x:number)overridable |
例如,可以用 PrecisePointsto 继承和覆盖 AbstractPointsto 的 HeapAllocationMerge 关系,实现更精确的分析:
1 | .comp AbstractPointsto{ |
类型参数化和继承
超级组件的类型参数可以在子组件声明中明确指定,下面定义了一个带参数 K 的子组件 B,用于实例化带参数 K 的超组件 A:
1 | .comp A<T> { .... } |
类型参数也可以用作基类,基于类型参数 T 选择性继承,A<T> 的实例定义继承的超级组件:
1 | .comp A<T> : T { ... } |
通过继承,可以实现复杂的组件实例化,注意这里要引入一个新的组件,因为参数 Graph<number> 不是简单的标识符:
1 | // 错误 |
编译指令 Pragma
允许直接在源码中设置命令行标志和配置,例如下面的代码将在调用 souffle 时指定 --legacy 标志:
1 | .pragma "legacy" |
有一些配置不能用命令行标志设置,因此也就不能用这种方法设置。
结语
想更深入地了解 Datalog 可以看看 Datalog and Recursive Query Processing,还有学长推荐的 Dimension Shift! 一起来学Datalog吧!,这方面我倒是没有扩展地去看;Doop 框架的提出可以看 Strictly Declarative Specification of Sophisticated Points-to Analyses,具体的指针分析实现可以参考 Pointer Analysis。
Doop 虽然很强大,但是学起来比较困难,而且我还没什么 Java 基础… 费劲。